how to: a geometric 3d bevel (obsolete)

This is a tutorial that covers basic 3d modeling and rendering. It demonstrates how to write a beveling algorithm, which takes a 2d polygon and extrudes it into a 3d shape, and includes the basics of lighting 3d objects.

**********************
NOTE! NOTE! NOTE! This algorithm has been obsoleted. There is a considerably improved one now available HERE. I'm leaving this one up because it has a simple shader and it also uses a different extrusion method, which could be combined with the clipping on the new algorithm, but the new clipper is vastly superior. I wouldn't touch this one.
**********************

DOWNLOAD. Java project written for Android. If you want to run the app, you will need to install the Android emulator and development environment.

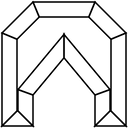
Input is provided as a list of points forming a 2d polygon. We'll run the example on a shape I call silo, a simple object that covers a number of properties we want to test against the algorithm.

The first step is to convert every two points on our initial polygon into a quadrilateral. Each new point is created the same way: Feed the algorithm 3 points, with the center point the one that we are generating the new point for. Treat each segment like a ray to determine the direction (flipping the direction will cause the new point to be extruded outside the polygon, instead of inside). With this direction info, find new segments that are parallel to the existing segments. Finally, determine where the segments intersect. The basic algorithm is implemented in the getBevelPoint() method of Bevel.java.

In ideal circumstances, this gives us an ideal bevel.

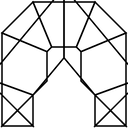
Unfortunately, these are rare cases. In all likelihood, the bevel depth was set high enough to extrude quads into each other, creating overlapping geometry.

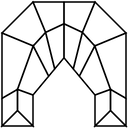
This brings us to the heart of the algorithm, which is clipping the overlaps. Conceptually, the problem is fairly simple. Imagine our object rotated on its side, so that we see two planes rising from the ground and intersecting. That line of intersection is the clip point, and we want to remove everything above it. The basic steps are these:

1. For each quad a, find its line segment of intersection with quad b.
2. Convert quad a into a 2d polygon, and convert quad b into a 2d polygon at the segment of intersection and up to infinity.
3. Subtract polygon b from polygon a.
4. Repeat for each quad that overlaps quad a.
5. Convert the resulting polygon a into a series of quads back in the original 3d space.

The algorithm is simple, but the implementation is extensive enough that it's easier to look at the source rather then a series of excerpts. The main loop happens in QuadClipper.java, which builds a QuadClipList.java for each intersection. The clip list relies on PolygonClipper.java for subtracting 2d polygons.

Now that we have a 3d model, let's take a couple extra minutes to light and shade it. This is a huge topic, but the basics are very simple: To light a 3d object, all you need is the surface normal and a light source. The normal is merely the vector perpendicular to your surface. In the case of a quadrilateral, the normal is found by taking the cross product of the diagonals, for example:

void setOn(final Quad q, final Surface s) {
mA.asVector(q.mPt[0], q.mPt[2]);
mB.asVector(q.mPt[3], q.mPt[1]);
s.mNormal.asCrossProduct(mA, mB);
s.mNormal.normalize();
}

and then measuring the distance to a light source:

private final double lightFrom(final Point3 normal, final Point3 light) {
return (normal.x*light.x + normal.y*light.y + normal.z*light.z) / (normal.length() * light.length());
}

Both methods are found in Render.java.

With the normals we can now light each surface of the model.

Finally, let's add a little shading to our lighting. The algorithm I wrote takes the average of the normals of all overlapping points, interpolates between them, then modulates by the distance to the center of the beveling (see SurfaceShader.java). This is just a variation on Phong shading, see references.

The interpolation method tends to produce uncomfortable edges where surfaces meet. The rendering could be greatly refined, but it's easier to get a smoother appearance merely by the introduction of additional geometry. For example, a low resolution sphere

shows much rougher lighting then a higher resolution one.

IMPROVEMENTS

The bevel algorithm needs refinement. Currently, there are cases where the new point produced is further out then the distance specified. In these cases, it should be limited to the distance and shortest lines drawn to the intersecting lines, creating a new quad. You can see this effect in the tip of the inner cutout of the silo shape. I confess I've sorta grown used to it, it made for good test cases.

The quad clipping breaks when pushed to extremes. This relates to how the line intersection between quads is found during clipping. The current method is rather ad hoc, with the edges of each shape being sent as rays to the other to see where they intersect and, when an intersection is found, some rules applied to find the line. This should be much more straightforward: Find the line of intersection between two planes, clip it to the quads in question.

During clipping, the quads are reduced to 2d by looking at the location of each intersecting segment endpoint and scaling based on proximity to the edge. This works fine for this particular application, where the the sides of the quad have the same Z value (i.e. the bottoms are always 0, and the tops are always the requested height). In a more complex environment this would break down, and you'd need to handle this by doing an actual 2d projection and performing your polygon subtraction on that.

When converting a 2d polygon back into 3d space, the results are simplified, since otherwise it's easy to create a large number of quads overlapping the same pixel. Right now this simplification is completely arbitrary, so it's entirely possible to end up with too many or too few resulting quads. It should be handled so that it's looking at the actual resulting pixels of each new quad, and combining as necessary.

REFERENCES

Segment to segment intersection (2d)
http://alienryderflex.com/intersect/

Segment to segment intersection (3d)
http://softsurfer.com/Archive/algorithm_0106/algorithm_0106.htm#dist3D_Segment_to_Segment()

Ray to triangle intersection (3d)
http://www.softsurfer.com/Archive/algorithm_0105/algorithm_0105.htm

Distance from point to segment (3d)
http://www.softsurfer.com/Archive/algorithm_0102/#dist_Point_to_Segment()

General all-around good intersection info
http://www.realtimerendering.com/intersections.html

Gouraud and Phong shading
http://www.nbb.cornell.edu/neurobio/land/oldstudentprojects/cs490-95to96/guo/report.html